Inside Gated Reality

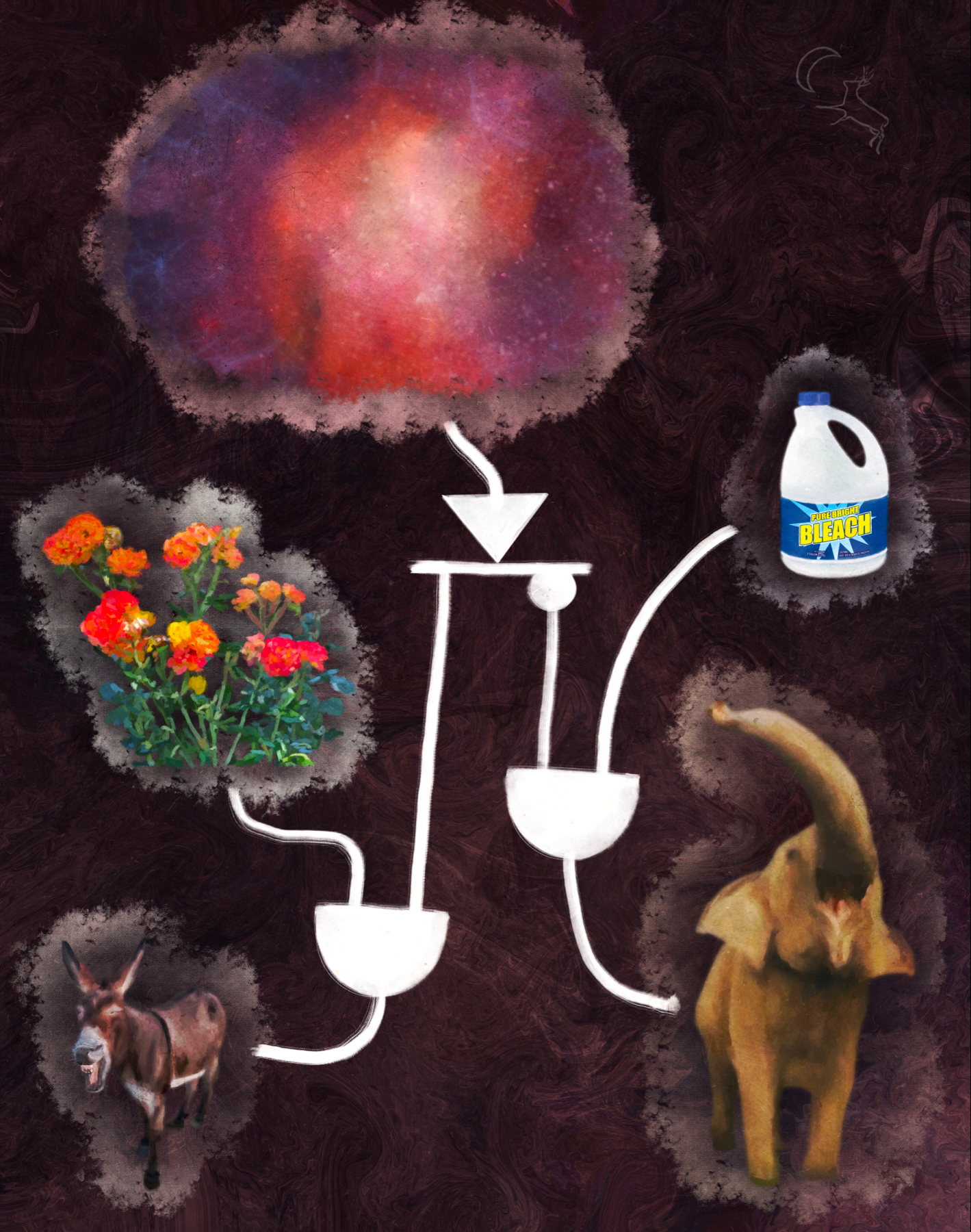
Breaking down just what the f$&k is going on in this diagram.

For those without a background in computer science (or electrical engineering, one would presume), the shapes with which this diagram has been composed are called logic gates. It's with these babies that one builds digital circuits. The typical CS student only really encounters them when learning Boolean algebra, as zeroes and ones are meant to be fed into the diagram as input, feed the various operations represented by the shapes, and come out the other end as output.

The only difference between the art and your typical logic gate diagram is the extension of the domain from {0,1} to {reality}. Let's go through it operation by operation to see how these gates function within the realm of metaphor.

The Input

Without input, we go nowhere. So, we'll feed some in at the top of the diagram. We'll mix in some additional input down the line, sans the arrowhead. The arrowhead indicates that this is where the flow of our diagram starts.

As far as our inputs go, this one is likely the most difficult to grok. What you see here is a depiction of the known universe. You'll recall I said the domain for this diagram would be {reality}. This was the best I could manage for representing that shit.

We want to send our input down multiple paths. To accomplish this, I chose to deploy a solid bar.

Our input connects to the top. Each connection made to the bottom of the bar shall receive our input (which, you'll recall, is no less than reality) in its entirety.

The First Path

Thus beginneth the leftmost path through the diagram. Let's add some more input. How about some roses?

Of course, we'll need to do something with our two inputs to make our diagram amount to more than just a gaggle of pretty pictures.

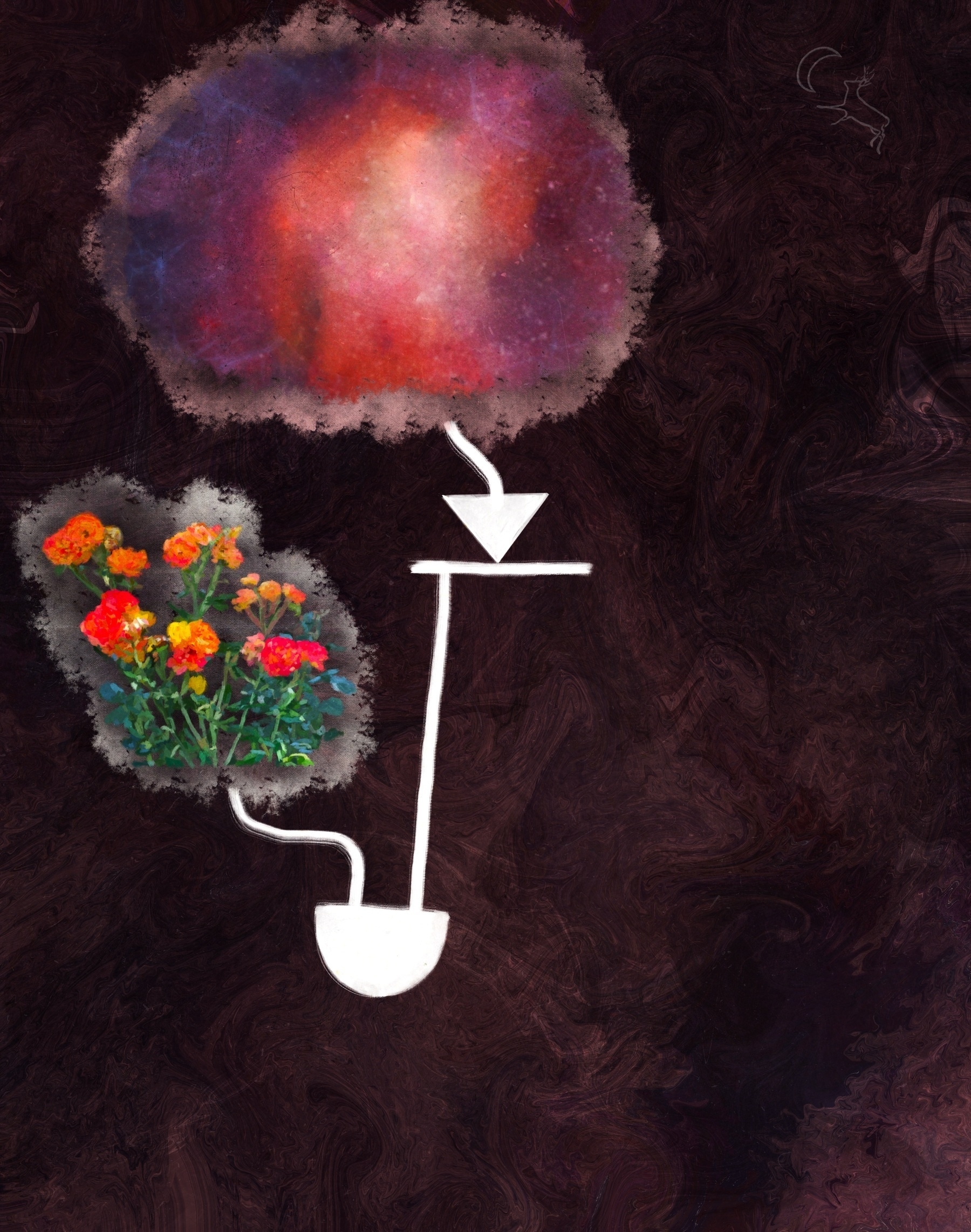
Finally, our first logic gate. This here half of a solid circle, ladies and gents, is an AND gate. Why is it called that? It performs an AND operation upon its input (which we always stick on the flat bit of the shape). Intimidating and unapproachable for all y'all unacquainted with boolean algebra, am I right? What if I tell you that AND is just what we CS f$&kers call addition when working with binary operands? Better, right?

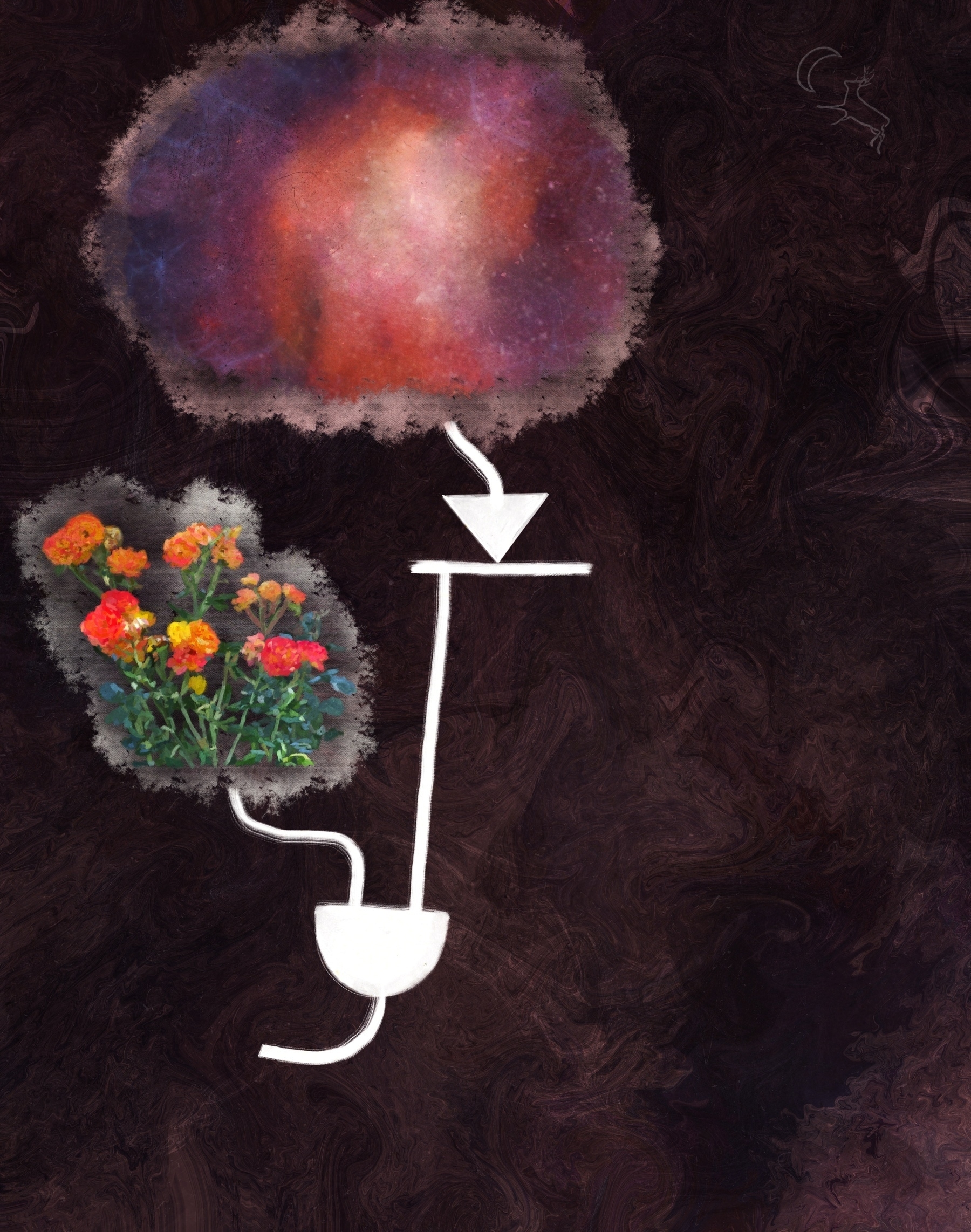
The result of the operation falls out of the curvy bit. In this case, we've added roses to reality. Sooo … let's see … carry the thorn … got it, the output of the AND gate would be a bit rosier reality. All this path is missing now is an output. How's about a donkey?

Yup, that'll do. This particular donkey is here to represent the DNC (or Democratic National Committee). More than that, he's braying, which is my way of indicating that this donkey is here to represent DNC messaging.

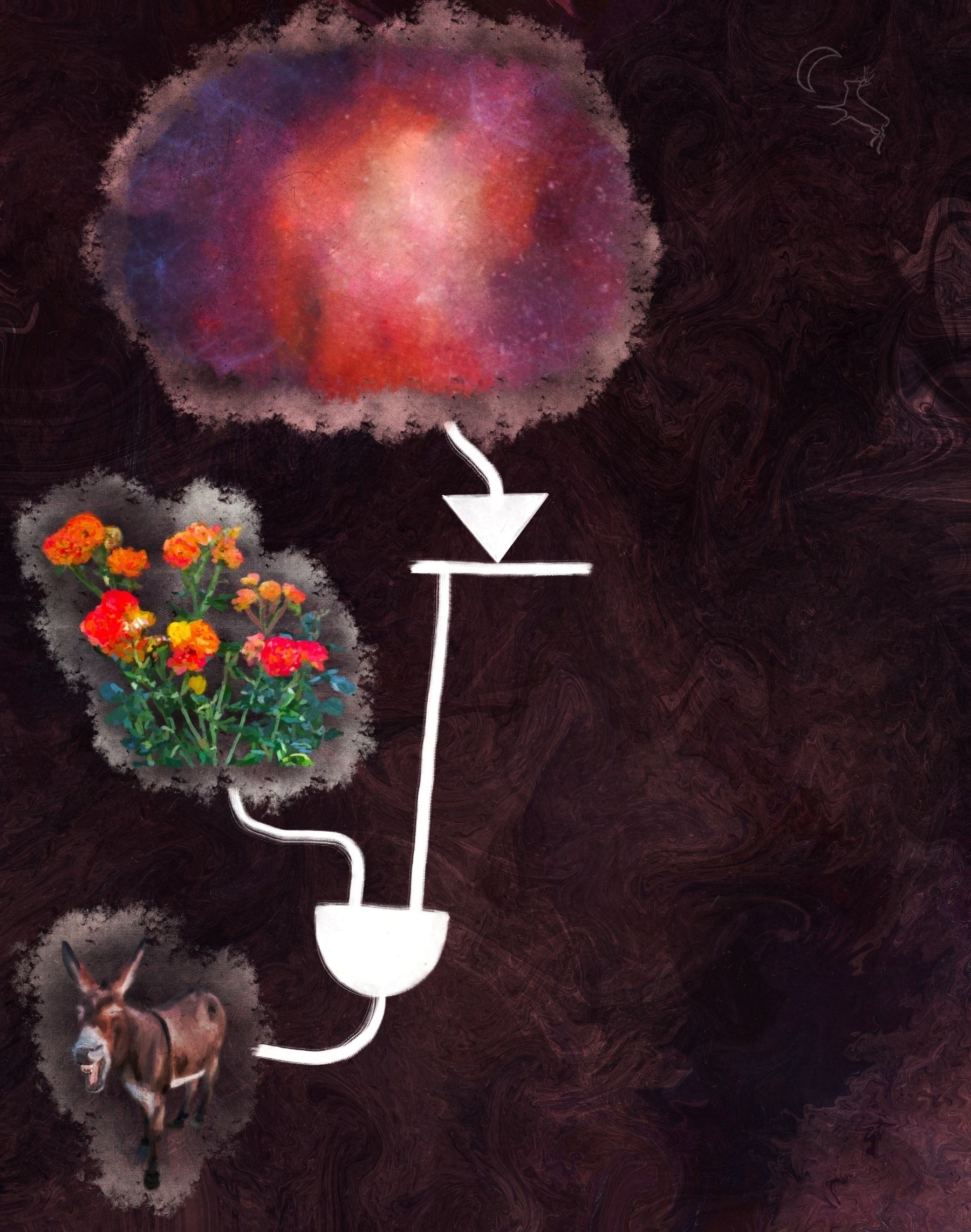
So, we stick the input up the donkey's bum to complete our path. We start up at the top with reality, we add some roses to fabricate a rosier reality than we started with, and we send that rosier reality through the donkey's innards to be deployed as messaging for the Democratic Party. Now, let's tackle the rightmost path, shall we?

The Second Path

Were you expecting another line? I bet you were expecting another line. Have you no memory of the completed diagram I showed you up top … what … like two minutes ago? Whatever, look … we probably could have drawn a line between the bar and the dot … had we wanted to look like doltish dot mishandling dweebs before our logic gate grokking peers. We needn't draw that line because this here dot happens to be a logic gate for a unary function (only one operand). This here dot is a NOT gate. Its only job is to invert whatever the f$&k it receives.

Like the line that launched the leftmost path, this dot receives the input fed into the top of the bar in its entirety. We'll draw a line out the bottom of the dot for carrying this inverted input.

If you're catching on, like … at all, then you'll recall that this input value happens to be reality. So, we feed reality into the NOT gate, acquiring inverted reality. How might one invert reality? Here, I'll show ya.

Let's say the NOT gate's function is 𝒚 = 𝐍𝐎𝐓(𝒙).

Let 𝒙 = Insurrectionists aiming to disrupt the transfer of power (from the demagogue desperately attempting to install himself at the head of an authoritarian regime rather than cede the office to the leader a nation chose for his replacement) launched an assault upon the Capitol (during which gallows were raised, mortal blows exchanged, and mortalities incurred) that was ultimately foiled by the brave men and women sworn to protect these sacred halls (and its occupants) from the threat of mob violence.

Now, if we feed 𝒙 into our 𝐍𝐎𝐓 function we can expect our result to belong to the same equivalence class as a value like 𝒚 = Patriots gathered together at the Capitol for the purpose of preventing the theft of a presidential election from a leader the people had re-elected (during which this peaceful gathering, of what one might almost describe as a gaggle of tourists, were subject to the physical abuse doled out by traitorous men and women forswearing their constitutional oaths) only to find this patriotic display twisted into a distorted narrative to serve as grounds for their persecution by the invisible machinations of the deep state. We good? Cool. Let's add more input and stir shit up.

There it is. So, what did we add?

What?

**slaps the screen with an analog pointer**

Come on, son. It's like you're not even trying. Stop mumbling. Sit up straight and open your eyes, for f$&k's sake (and for the sake of all of f$&k's close relations, come to think of it). I wrote what it is on the bottle's label.

're white bleach. Yes, that's right. Where we added roses before, we are now adding pure white bleach.

And, just as before, we shall send our two inputs through an AND gate.

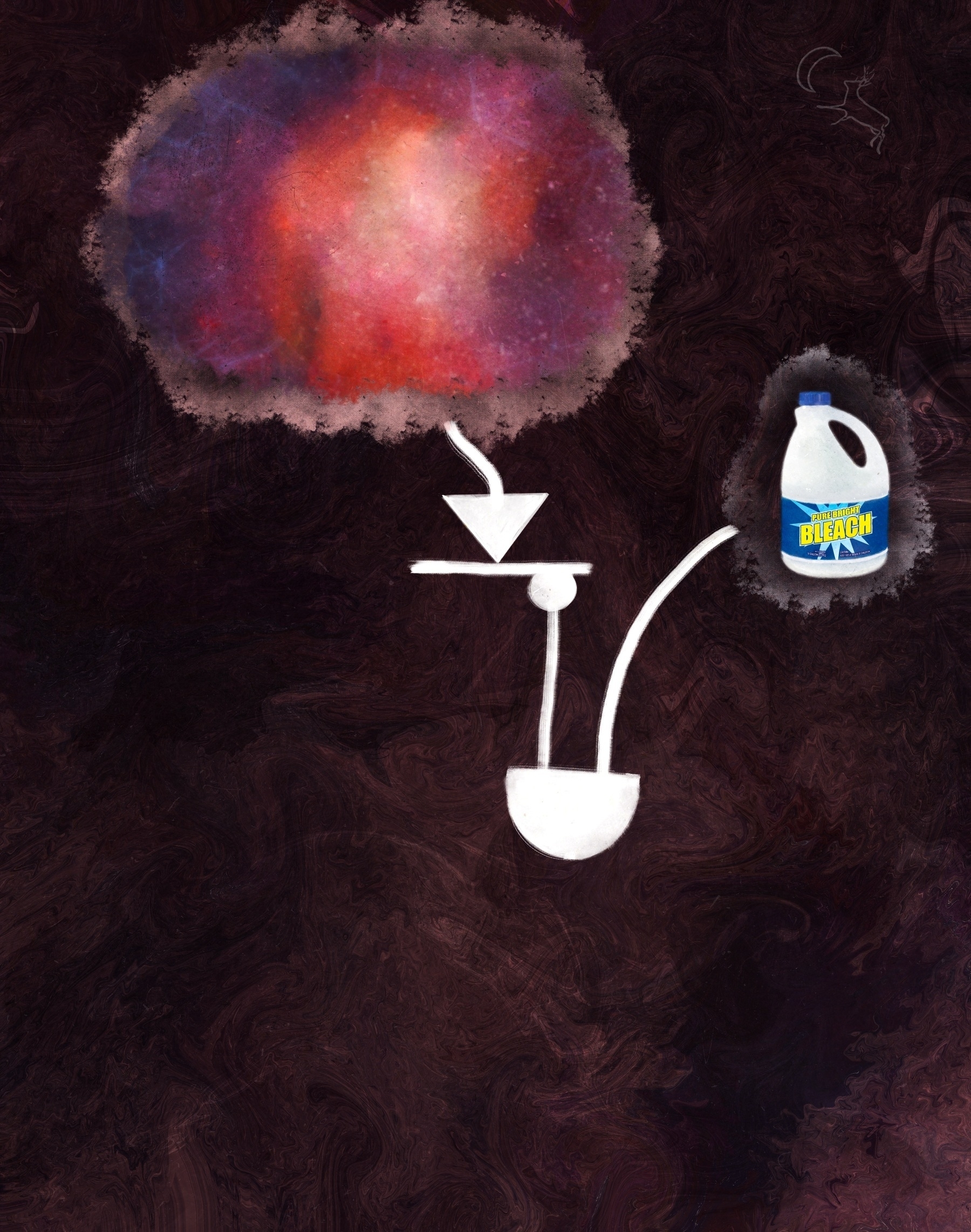
So, we'll be taking our inverted reality and our pure white bleach, running them through an AND gate, and receiving the sum out the gate's curvy bit.

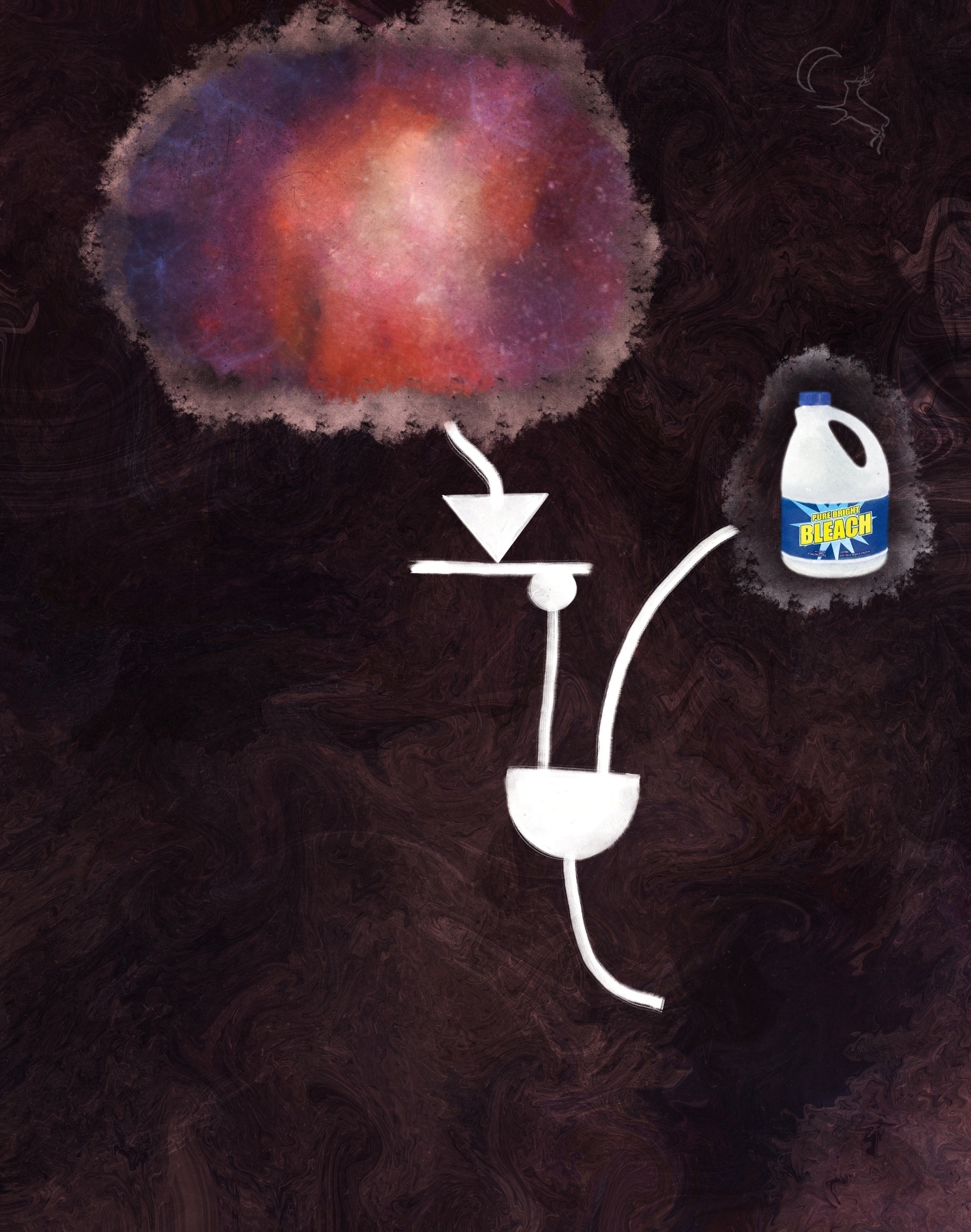
So, what comes out of this gate? Well, what do we imagine would be the most common use for pure white bleach. I imagine that, were Richard Dawson standing before an audience of Family Feud, and he was all, "Name a popular use for pure white bleach," the first contestant asked would be all, "in the laundry room when you're washing your whites." Then, Dawson would be all, "Show me 'washing whites'" and the energy in the room would spike as the panel for the number one answer flipped itself over to reveal "Washing Whites."

So, with that in mind, if we take our inverted reality and stir in copious amounts of pure white bleach, we'll have ourselves whitewashed, inverted reality.

Now that we got it, what shall we do with it? We shoved our output up donkey's bum to finish off the leftmost path. Shall we choose another critter, you know, for symmetry? How about an elephant?

Boom. Elephant beetches.

**copies the bit about the donkey**

**pastes the copied bit below**

**globally substitutes three words and a letter**

This particular elephant is here to represent the RNC (or Republican National Committee). More than that, he's trumpeting, which is my way of indicating that this elephant is here to represent RNC messaging.

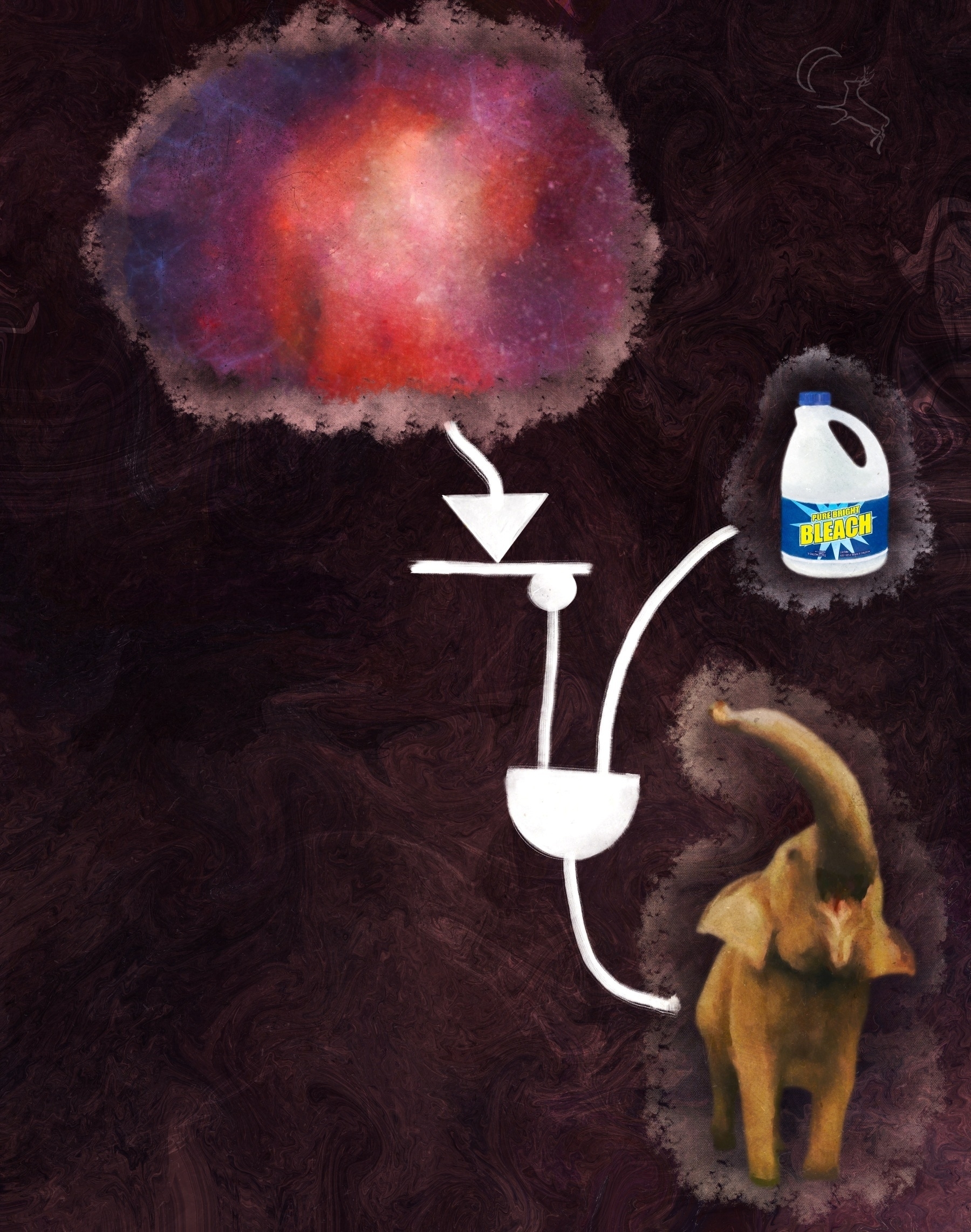
You knew what was coming. We stick this input up the elephant's bum and path numero deux est finito (three-languages-I-don't-speak-mic-drop). As with the leftmost path, we start up at the top with reality. This time, we invert that reality and add some bleach to whitewash said inverted reality. This whitewashed, inverted reality is then loaded into the elephant's tail adjacent orifice to journey through the digestive tract, exiting near the trunk for deployment as messaging for the Republican Party.

In Closing

Feel free to insert your own summary paragraph here. I don't feel like writing one. Peace. ☾𐂂 out.